2018 THEMIS SCIENCE NUGGETS

Magnetosheath Propagation Times for Solar Wind Directional Discontinuities

by A. A. Samsonov
Mullard Space Science Laboratory, UCL, UK

Introduction

Solar wind directional discontinuities (DD, i.e., tangential or rotational discontinuities) may bring significant changes in the interplanetary magnetic field (IMF) and solar wind plasma parameters to the Earth’s magnetosphere. For example, the arrival of a DD associated with a southward IMF turning at the dayside magnetopause can initiate magnetic reconnection and enable solar wind mass, momentum, and energy to enter the magnetosphere. Consequently, we would like to predict the precise time when a DD observed by a solar wind monitor at the Lagrangian point L1 will reach the subsolar magnetopause. Although we do not have a permanent monitor at the subsolar magnetopause, we can use ground magnetometer or radar observations to estimate this delay time because southward IMF turnings elicit rapid responses in magnetospheric-ionospheric electric currents and magnetospheric convection. Past studies have shown that the delay from the time when a solar wind DD is estimated to reach the subsolar bow shock to the time when the first ground response is about 10-16 min. A portion of this delay results from the time required for discontinuities to cross the magnetosheath. Near the Sun-Earth line, the magnetosheath is typically about 3 Earth radii (RE) thick.With a velocity of 400 km/s, the solar wind could traverse this distance in less than 1 min. Although we know that the magnetosheath flow velocity is smaller than that in the solar wind, we do not know exactly how much this increases the propagation time. Determining the time to traverse the magnetosheath is the objective of this study.

Flow Deceleration in the Magnetosheath

Samsonov et al. (2018) used the Space Weather Modeling Framework (SWMF) global MHD model available through the Community Coordinated Modeling Center (CCMC) runs on request at NASA/GSFC to conduct the simulations. For the solar wind input conditions, they use THEMIS B observations of the event on 7 August 2008 studied previously by Samsonov et al. (2017). This event is characterized by an abrupt Bz change from +3 to -2 nT at the DD. The other solar wind parameters are rather typical for a slow solar wind, e.g. the upstream velocity Vx = -346 km/s.

Figure 1. (a) Magnetopause (triangles), directional discontinuity (stars), and bow shock (squares) positions on the Sun-Earth line as functions of time. Red indicates positions determined from the maximum in |j|, black triangles mark the magnetopause as the boundary between open and closed field line topologies, green triangles mark the stagnation position where Vx = 0, blue stars indicate the DDs determined from Bz = 0. (b) Positions of the DD determined by the maximum in |j| (black triangles) and calculated from the initial Vx profile (red line). Vertical dashed lines indicate magnetopause and bow shock positions.

Figure 1 shows the positions of the magnetopause, DD front, and bow shock on the Sun-Earth line as functions of time. When the DD reaches the bow shock, the magnetopause and bow shock are located ~12 and 17 RE upstream from Earth respectively. The figure illustrates the deceleration of the DD during its propagation through the dayside magnetosheath. The DD passes through the first half of the magnetosheath width in only 3 min, but requires 12 min to traverse the second half, gradually decelerating as it approaches the magnetopause. In fact, both tangential and rotational discontinuities propagate with the flow velocity (but for rotational discontinuities this is strictly true only in the direction perpendicular to magnetic field), therefore we can estimate the magnetosheath propagation time of the DD using the initial velocity profile. The red line in Figure 1b displays the propagation time calculated from the velocity profile. This time agrees perfectly well with the simulated propagation of the DD front indicated by black triangles.

Propagation Time as a Function of Solar Wind Parameters

Samsonov et al. (2018) studied velocity profiles along the Sun-Earth line and showed that for typical solar wind conditions and a reasonably small IMF magnitude, the velocity nearly linearly decreases from the bow shock to the magnetopause. This property can be used to calculate magnetosheath propagation times. The following expression has been obtained:

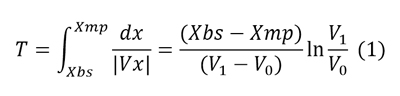
Here, Xbs and Xmp are bow shock and magnetopause positions, and V0 and V1 are the velocities immediately upstream of the magnetopause and downstream of the bow shock respectively. The magnetosheath thickness and V1 can be calculated from the upstream solar wind parameters. The cutoff speed V0 does not have a straightforward definition. In MHD theory, V0 for a southward IMF case can be obtained from the reconnection velocity (estimated as ~0.1 VA, where VA is Alfven speed near the subsolar magnetopause), but V0 = 0 for a northward case when reconnection occurs behind the cusps. However, in reality the magnetopause is always in motion with a typical speed of about 10-20 km/s. Assuming V0 = 10 km/s and solar wind conditions for the event on 7 August 2008 mentioned above, we get a propagation time of 11.4 min in agreement with observations of this event. Using (1), Samsonov et al. (2018) studied the dependence of the propagation time on the solar wind velocity and IMF Bz (By).

Timing the Response to Directional Discontinuities Seen in Ground Observations

To confirm their numerical predictions, Samsonov et al. (2018) considered the response seen by ground observatories to solar wind DD. They chose 35 events with both northward and southward IMF turnings observed by THEMIS probes B and C in the solar wind at locations of 10–15 RE upstream from the bow shock. Using of THEMIS probes in the solar wind instead of ACE or Wind located near L1 is preferable because the time lag from THEMIS to the subsolar bow shock can be calculated more accurately. The time of the ground response was determined from variations in the PCN index: the PCN index increases in response to southward IMF turnings and decreases in response to northward turnings. Samsonov et al. (2018) calculated the time delays of the ground response relative to the time when the DD was predicted to interact with the subsolar bow shock.

Figure 2. Time delays of ground response to both southward and northward interplanetary magnetic field turningscounted from the contact of directional discontinuities with the subsolar bow shock. The red line represents the least squares fit.

Figure 2 shows the time delays as a function of the solar wind speed. The red line represents an exponential fit to all points. In general, the observations confirm that the time delay decreases with increases in the solar wind speed. Moreover, the results in Figure 2 quantitatively agree with MHD simulations for similar solar wind conditions. Although strictly speaking the propagation time across the magnetosheath and the time delay of the ground response to features reaching the bow shock must be different, Samsonov et al. (2017) suggested that the time interval from the DD interacting with the subsolar magnetopause to the first ground response is only about 1–2 min, i.e. the difference between the two times is small.

Conclusion

We summarize the main results below.

Reference

Samsonov, A. A., Sibeck, D. G., Dmitrieva, N. P., Semenov, V. S. (2017). What happens before a southward IMF turning reaches themagnetopause? Geophysical Research Letters, 44, 9159–9166. https://doi.org/10.1002/2017GL075020.

Samsonov, A. A., Sibeck, D. G., Dmitrieva, N. P., Semenov, V. S., Slivka, K. Y., Šafrankova, J., Němeček, Z. (2018) Magnetosheath propagation time of solar wind directional discontinuities. J. Geophys. Res. Space Physics, 123, 3727–3741, doi:10.1029/2017JA025174, 2018.

Biographical Note

Andrey Samsonov is a scientist at the Mullard Space Science Laboratory/University College London. His fields of scientific interest are: solar wind – magnetosphere interactions, magnetosheath and magnetopause, interplanetary shocks, and MHD modeling. Now he is applying his knowledge and expertise in preparations for the forthcoming SMILE mission.

Please send comments/suggestions to
Emmanuel Masongsong / emasongsong @ igpp.ucla.edu